| Whatsapp Group |
| Whatsapp Channel |
| Telegram channel |
Functions are relations in which each input has a specific output. Let’s learn about two of the most commonly used types of functions i.e., Modulus and Signum functions with examples for better understanding.
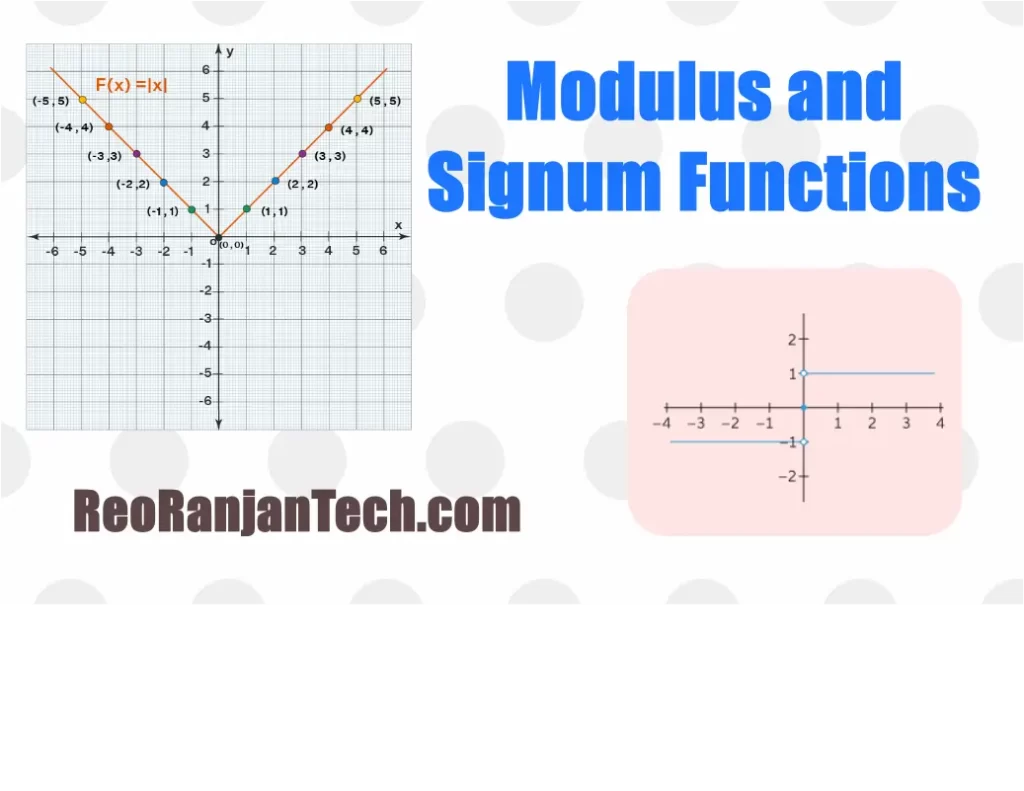
A modulus function gives back an integer or variable’s absolute value. It generates the magnitude of the variable count. An absolute value function is another name for it. No matter what input was provided to this function, the outcome is always positive (+). It is represented as y = |x|. Plotting such graphs is also a simple process, where the domain is all input values, say x (all real numbers), and the range is all function values (y = f(x) = all positive real numbers and 0).
The Signum function, which has attributes +1 for positive input values and -1 for negative input values, assists in finding the sign of a real value function. The signum function has several applications in physics and engineering and is widely used in AI for prediction.
Let us learn more about the Modulus and Signum function, then the steps to find the inverse function.
Concepts of Modulus Function
If each element of a non-empty set X has just one image or range to a non-empty set Y, the relation ‘f’ is called a function. Modulus function f(x) of x is defined as follows:
f(x) = |x|
Or
y = |x|
Where f: R→R and x ∈ R
And |x| gives modulus of x.
If x is positive, then the function f(x) returns only x. If x is negative, the magnitude of x will be the output of x. As a result, we can rename the modulus function:
f(x)= x or -x,
if x≥0 or x<0 respectively
According to the aforementioned statement, the modulus function accepts the real value if x is higher than or equal to 0. If the value of x is less than zero, the function minus the actual values. Let us look at few examples to help us understand:
If x = -5, then y = f(x) = – (-5) = 5, since x is less than zero
If x = 10, then y = f(x) = 10, since x is greater than zero
If x = 0, then y = f(x) = 0, since x is equal to zero
Modulus Function Graph
Let us now look at how to graph a modulus function. Consider x to be a variable with values ranging from -5 to 5. When the modulus is calculated for positive values of ‘x,’ the line plotted in the graph is ‘y = x,’ and when the modulus is calculated for negative values of ‘x,’ the line displayed in the graph is ‘y = -x.’
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) = |x| | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | 5 |
Modulus Function Graph:
Concepts of Signum Function
Let us learn more about the signum function and its graph.
What Is Signum Function?
The signum function returns the sign for the given x values. For x values greater than zero, the output is +1, for x values less than zero, the output is -1, and for x values equal to zero, the output is zero.
Sgm(f(x))= +1, -1 or 0,
if x>0, x<0 or x=0 respectively.
The signum function is an odd function that differs from the Trigonometric sine function.
Graph of Signum function
Simply entering some real number values and getting their corresponding images is the simplest way to construct the graph of any real-valued function. We can plot the input and output values on a graph if we have both of them.
Let’s look at a few example sets to draw the graph of the Signum function.
sgn(x)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| sgn(x) | -1 | -1 | -1 | 0 | 1 | 1 | 1 | 1 |
Consequently, the graph of the Signum function appears as follows:
Read More:
- Best websites for government job preparation in India
- Adani turns into the world’s second richest man after overtaking Amazon’s Jeff Bezos and luxurious king Bernard Arnault
- How to use Grammarly in Google Docs
- How Firewall Protects a Network From Attacks